What is Flash Attention?
Introduction
Flash Attention1 is an IO-aware exact attention algorithm that uses tiling to reduce the number of memory reads/writes between GPU high bandwidth memory (HBM) and GPU on-chip SRAM.
It has been widely used in LLM inference and training, and is the default attention backend in modern serving engines like SGLang, vLLM, etc.
Naive Attention Calculation
Before we figure out how Flash Attention works, let’s first take a look at the naive attention calculation.
\[\begin{align} \text{attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}\left(\frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{d}}\right)\mathbf{V} \end{align}\]where:
- \(\mathbf{Q}\), \(\mathbf{K}\), \(\mathbf{V}\) are the query, key, and value matrices, respectively.
- \(\mathbf{d}\) is the dimensionality of each attention head (used for scaling).
Key Challenge: The intermediate result of \(\mathbf{Q}\mathbf{K}^\top\) can be extremely large. For a sequence length \(n\), the matrix \(\mathbf{Q}\mathbf{K}^\top\) has dimensions \(n \times n\), leading to a memory footprint that scales as \(O(n^2)\). As sequence lengths increase (common in large language models or multimodal applications), GPU memory usage grows quadratically, making this approach inefficient and resource-intensive.
It’s intuitive to think that we can using Tiling to split the large matrix into smaller ones and compute them in parallel. However, this approach is hindered by the fact that the softmax operation is hard to be parallelized.
Softmax Optimization
Naive Softmax equation
\[\text{softmax}(\mathbf{x_i}) = \frac{e^{x_i}}{\sum_{j=1}^{n} e^{x_j}}\]Above equation is the naive softmax equation. When \(\mathbf{x_i} > 11\), \(e^{x_i}\) will overflow since FP16’s maximum value is 65504 while \(e^{12} = 162754.791419\)
The code implementation of naive softmax is as follows:
def naive_softmax(x):
"""Naive Softmax implementation, prone to overflow in FP16."""
# Compute exponentials
exp_x = torch.exp(x)
# Compute sum of exponentials
sum_exp_x = torch.sum(exp_x)
# Normalize
return exp_x / sum_exp_x
Safe Softmax: 3-pass
We need to introduce safe softmax to avoid overflow.
\[\text{safe-softmax}(\mathbf{x_i}) = \frac{e^{x_i-m}}{\sum_{j=1}^{n} e^{x_j-m}}, m = \max(\mathbf{x_i})\]We can compute the attention output with Safe Softmax by 3-pass2:

3-pass softmax
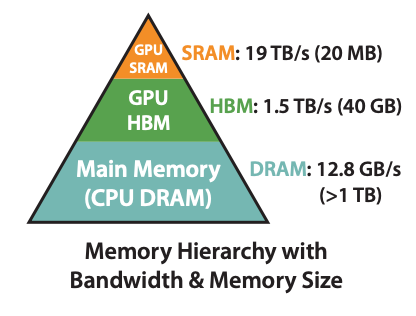
HBM-SRAM memory hierarchy
With this, we will read \(\mathbf{Q}\) and \(\mathbf{K}\) three times given SRAM cannot fit them all at once. It’s not efficient since access HBM is expensive.
The code implementation of safe softmax is as follows:
def safe_softmax_three_pass(x):
"""Safe Softmax implementation using three passes to avoid overflow."""
# Pass 1: Compute the maximum value for numerical stability
m = torch.max(x)
# Pass 2: Compute the exponentials
exp_x = torch.exp(x - m)
# Pass 3: Compute the sum and normalize
sum_exp_x = torch.sum(exp_x)
return exp_x / sum_exp_x
Online Softmax: 2-pass
Online softmax3 is a technique that can be used to reduce the number of passes required to compute the softmax.

The code implementation of online softmax is as follows:
def online_softmax(x):
"""Online Softmax implementation using two passes for efficiency."""
# Pass 1: Compute maximum and sum of exponentials in one traversal
m = float('-inf') # Current maximum
s = 0.0 # Sum of exponentials
for xi in x:
m_old = m
m = max(m, float(xi))
s = s * torch.exp(torch.tensor(m_old - m)) + torch.exp(xi - m)
# Pass 2: Normalize
return torch.tensor([torch.exp(xi - m) / s for xi in x])
We can clearly see that the first two passes in 3-pass softmax are fused into one pass, which is fairly good, but can we do better?
Flash Attention V1: 1-pass
The answer is no for fuse 2 passes into 1 pass for the computation of: \(\text{softmax}(\mathbf{Q}\mathbf{K}^\top)\), however, what we need is \(\text{softmax}\left({\mathbf{Q}\mathbf{K}^\top}\right)\mathbf{V}\)
Flash Attention is the technque which can fuse the computation of: \(\text{softmax}\left({\mathbf{Q}\mathbf{K}^\top}\right)\) and \(\mathbf{V}\) into one pass.
Here is the algorithm: 
The Flash Attention Author derived the algorithm hence the output only depends on \(d_i'\), \(d_{i-1}'\), \(m_i\), \(m_{i-1}\) and \(x_i\), thus we can fuse all computations in Self-Attention in a single loop.
The code implementation of naive softmax is as follows:
def flash_attention_v1(Q, K, V):
"""
FlashAttention V1 implementation with single-pass computation.
Fuses Softmax(QK^T)V into one loop without storing S or P.
Args:
Q, K, V: Query, Key, Value matrices of shape (seq_len, head_dim)
Returns:
Output of attention: (seq_len, head_dim)
"""
seq_len, head_dim = Q.shape
scale = 1.0 / (head_dim ** 0.5) # Scaling factor 1/sqrt(d)
# Initialize output and running statistics
O = torch.zeros_like(Q) # Output
l = torch.zeros(seq_len, dtype=torch.float32, device=Q.device) # Sum of exponentials (d_i')
m = torch.full((seq_len,), float('-inf'), device=Q.device) # Max values (m_i)
# Single pass over sequence length
for i in range(seq_len):
# Compute Q[i] * K^T for row i
S_i = torch.matmul(Q[i:i+1], K.transpose(-1, -2)) * scale # Shape: (1, seq_len)
# Online Softmax for row i
m_i = torch.max(S_i) # Current max (m_i)
m_old = m[i] # Previous max (m_{i-1})
m_new = torch.maximum(m_old, m_i) # Update max
l_old = l[i] # Previous sum (d_{i-1}')
# Update sum of exponentials (d_i')
exp_diff = torch.exp(m_old - m_new)
exp_S = torch.exp(S_i - m_new)
l_new = l_old * exp_diff + torch.sum(exp_S)
# Update output: O[i] = O[i] * exp(m_old - m_new) + exp(S_i - m_new) * V
O[i] = O[i] * exp_diff + torch.matmul(exp_S / l_new, V)
# Update statistics
m[i] = m_new
l[i] = l_new
# Final normalization
O = O / l.unsqueeze(-1)
return O
Flash Attention V1: Tiling
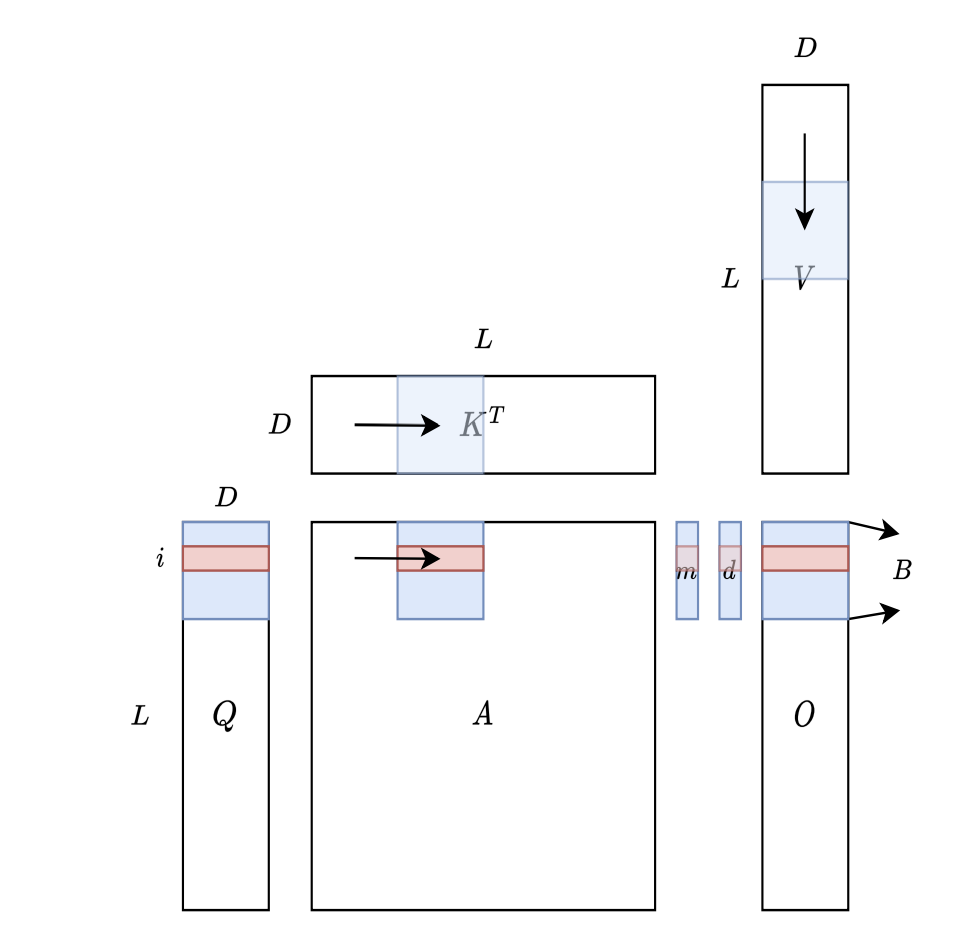
After we fused all computations in Self-Attention in a single loop, we can use Tiling to split the large matrix into smaller ones to fully levarage the speed of GPU SRAM.
From the diagram above, we can see that \(Q\), \(K\) and \(V\) has been split into blocks, and we can load them onto SRAM once to compute the attention output in the kernel.
Hence saved the intermediate results of \(S\) and \(P\) in HBM, and also reduced the IO Access from HBM to SRAM.
The code implementation of naive softmax is as follows:
def flash_attention_v1_tiling(Q, K, V, tile_size=128):
"""
FlashAttention V1 implementation with tiling to leverage SRAM.
Fuses Softmax(QK^T)V into one kernel with tiled computation.
Args:
Q, K, V: Query, Key, Value matrices of shape (seq_len, head_dim)
tile_size: Size of each tile for tiling computation
Returns:
Output of attention: (seq_len, head_dim)
"""
seq_len, head_dim = Q.shape
d = head_dim # Head dimension for scaling
scale = 1.0 / (d ** 0.5)
# Initialize output and normalization statistics
O = torch.zeros_like(Q) # Output
l = torch.zeros(seq_len, dtype=torch.float32, device=Q.device) # Sum of exponentials
m = torch.full((seq_len,), float('-inf'), device=Q.device) # Max values
# Tile over sequence length for Q and K
for i in range(0, seq_len, tile_size):
# Tile boundaries for Q
i_start = i
i_end = min(i + tile_size, seq_len)
# Load Q tile into SRAM
Q_tile = Q[i_start:i_end]
for j in range(0, seq_len, tile_size):
# Tile boundaries for K and V
j_start = j
j_end = min(j + tile_size, seq_len)
# Load K and V tiles into SRAM
K_tile = K[j_start:j_end]
V_tile = V[j_start:j_end]
# Compute S = QK^T / sqrt(d) for the tile
S_tile = torch.matmul(Q_tile, K_tile.transpose(-1, -2)) * scale
# Online Softmax within the tile
m_tile = torch.max(S_tile, dim=-1, keepdim=True)[0]
exp_S = torch.exp(S_tile - m_tile)
l_tile = torch.sum(exp_S, dim=-1, keepdim=True)
# Update global statistics
m_old = m[i_start:i_end, None]
m_new = torch.maximum(m_old, m_tile)
l_old = l[i_start:i_end, None]
l_new = l_old * torch.exp(m_old - m_new) + l_tile
# Update output: O = O * exp(m_old - m_new) + exp(S - m_new) * V
O[i_start:i_end] = O[i_start:i_end] * torch.exp(m_old - m_new).squeeze(-1)
O[i_start:i_end] += torch.matmul(exp_S / l_new, V_tile)
# Update m and l
m[i_start:i_end] = m_new.squeeze(-1)
l[i_start:i_end] = l_new.squeeze(-1)
# Final normalization
O = O / l.unsqueeze(-1)
return O